我們當開啟一個一個存檔或者是建立一個存檔過程中
一般就是經典的存檔名稱
世界型別還有是否允許作弊的選項
但是在這背後有沒有想過一些問題
世界是如何被生成的呢
我們今天就從底層邏輯方面去探討這些東西
文章具體內容多數引用知乎wiki
第一
我們現在探討一些關於噪聲函式的方面內容
柏林噪聲函式,又稱噪聲函式
在我的世界生成地形方面起到了十分重要的作用
就比如說是在材質紋理的渲染等方面
一些我的世界比較著名的bug也是出自這個之手
比如“邊境之地”
我們先來解釋一下柏林噪聲函式的定義
柏林噪聲 (Perlin noise )指由Ken Perlin發明的自然噪聲生成演算法 。一個噪聲函式基本上是一個種子隨機發生器。它需要一個整數作為引數,然後根據這個引數返回一個隨機數。如果兩次都傳同一個引數進來,它就會產生兩次相同的數。這條規律非常重要,否則柏林函式只是生成一堆垃圾
我們常說的地圖種子就是指柏林函式裡的種子輸入,“如果兩次都傳同一個引數進來,就會生成兩次相同的數”
可以說為什麼我們每次輸入相同種子都會出現相同地形的原因
從本質上來說,柏林噪聲函式
就是個隨機生成器,我的世界裡的地形就是這個函式隨即生成
我們眾所周知的都是知道我的世界的地形是一塊一塊的區塊拼接起來的
具體的敘述
噪聲(Noise)實際上就是一個隨機數生成器,當然,這是一種偽隨機(現實世界中的真隨機在計算機中不存在)。我們所看到的那些黑白噪聲圖,實際上是隨機數對映到0和1之間產生的灰度圖。隨機本身就是不同,那為什麼還需要不同的隨機?
普通噪聲(隨機數生成器)的問題在於,它實在太過於隨機,毫無規律可言(如圖1所示)。在上個世紀80年代,柏林噪聲的發明者 Ken Perlin 當時正在參與迪士尼的經典電影電子世界爭霸戰(TRON)的製作。他想用噪聲來模擬逼真的隨機效果,但對最終產生的不自然的效果很不滿意。在現實世界中,儘管很多自然現象(如山脈起伏、大理石紋理等)是隨機的,但隨機之中蘊含著規律,普通噪聲很難體現出這種亂中有序的效果。(引知乎使用者阿虎)
即
選取隨機點,給定隨機值給定點位的梯度(用插值函式標識)根據隨機點的值與梯度計算出為賦值位置的數值在這一過程中Perlin Noise使用一些特殊的處理策略保證生成的資料偽隨機並且連續
很簡單的數學函式原理
說明白點,就是在設定的是一個函式
這個函式的表示式就是特殊的處理方式
隨機點代表定義域
反饋的值在進行運算生成新的數值
從而達到生成地形的目的
一下為函式生成原理
public double perlin(double,x,double,y,double,z,):
這是最基本的柏林函式式子
想當然我們看到這個
可能會莫名想起在遊戲裡面看到的f3
沒錯,xyz說白了就是你生成世界的媒介,每一塊都有具體座標就是這樣來的
但是有沒有想過一個問題
double函式雖然說是極為大的數字
可以說是天文數字,我們可以看看具體在java中的數值
[-1.79769313486231570e+308,-4.94065645841246544e-324] ∪ [4.94065645841246544e-324,1.79769313486231570e+308]
說具體點就是2的正負1024次方
但是但是,前提是這個數字還是有最終臨界的
我們知道我的世界裡面是有tp指令的
當然,麻將肯定是想到了這個問題,其實在如今版本基本不會看到這個情況了
但是在遠古版本還是會有這樣情況出現的
notch在原先版本沒有設定tp指令的情況下還是知道到達這個數字的情況是怎麼樣的
所以說我們可以將這個天文數字稱之為xyz座標無限
這是很具體的比喻
因為的確就是座標無限
我們可以知道
其實我的世界地形的確就像是天文數字一樣,才會出現崩潰的現象
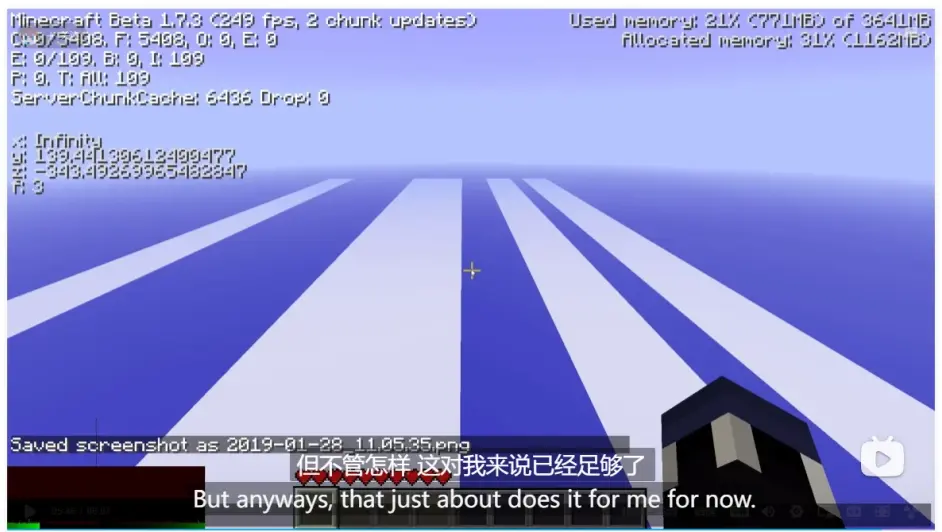
我們可以在這個視訊裡面看到,x座標是無限
所以說其實notch早在遠古其實就想到了這種情況
在本質上來說,或者是在早期遊戲裡面我們可以看到的是
我的世界其實在原本的單人遊戲就只是個內建伺服器
在1.7.10版本如果遊戲突然出現崩潰的情況就會出現關閉內建伺服器的字樣
其實客戶端只是單純的進行渲染和輸出,真正的內容展現在服務端
文章不去設計關於底層程式碼層面的內容
當然去具體的描述世界生成的流程
具體的就像是不斷地採集點
引用柏林函式的內容
這段程式碼以二維柏林噪聲為例,描述了確定一個點梯度值的過程。梯度表中的值都是隨機生成的,通過對點的
座標分別進行計算,可以得到點的梯度(即一個二維向量)。確定一點的梯度值並不止這一種方法,另一種可行方法之後會提到。
在一維柏林噪聲中,各個整點的梯度就是斜率,所以我們可以不依賴梯度表,將排列表中所取到值直接作為梯度即可。因為排列表中的值是亂序的,所以有良好的隨機性,且對於同樣的輸入,它的輸出都相同,偽隨機性也得以保留。在Ken Perlin的經典噪聲演算法中,使用的排列表是由數字0到255雜湊組成的。
static int[] perm = {151,160,137,91,90,15,
131,13,201,95,96,53,194,233,7,225,140,36,103,30,69,142,8,99,37,240,21,10,23,
190, 6,148,247,120,234,75,0,26,197,62,94,252,219,203,117,35,11,32,57,177,33,
88,237,149,56,87,174,20,125,136,171,168, 68,175,74,165,71,134,139,48,27,166,
77,146,158,231,83,111,229,122,60,211,133,230,220,105,92,41,55,46,245,40,244,
102,143,54, 65,25,63,161, 1,216,80,73,209,76,132,187,208, 89,18,169,200,196,
135,130,116,188,159,86,164,100,109,198,173,186, 3,64,52,217,226,250,124,123,
5,202,38,147,118,126,255,82,85,212,207,206,59,227,47,16,58,17,182,189,28,42,
223,183,170,213,119,248,152, 2,44,154,163, 70,221,153,101,155,167, 43,172,9,
129,22,39,253, 19,98,108,110,79,113,224,232,178,185, 112,104,218,246,97,228,
251,34,242,193,238,210,144,12,191,179,162,241, 81,51,145,235,249,14,239,107,
49,192,214, 31,181,199,106,157,184, 84,204,176,115,121,50,45,127, 4,150,254,
138,236,205,93,222,114,67,29,24,72,243,141,128,195,78,66,215,61,156,180};
可以看到在柏林函式裡邊的採點是要又255組組成
具體的取樣原理在不具體展開
感興趣的可以去知乎瞭解
說到底就是不斷地採值去計算
最簡單粗暴的理解

在這張早期反編譯的圖片裡面我們可以清楚的看到地形生成的複雜程度
這僅僅只是群系方面的程式碼
而且在柏林函式中也包含具體的灰度值等內容,由於生成機制過於複雜
就好比立體幾何中平面向量的應用

柏林噪聲函式生成的晶體格
有沒有很二維碼
當你把噪聲函式疊加的時候,你可能想了解每次具體使用了什麼振幅和頻率。上面一維的例子對於每個連續疊加的噪聲函式使用了兩倍的頻率和二分之一倍的振幅。這個太普通了,事實上太普通,以至於很多人甚至從來都沒有考慮過使用其他什麼。儘管如此,你可以通過在每步使用其他的頻率和振幅來建立不同特徵的柏林噪聲函式。例如,為了建立一個平滑滾動的丘陵,你可以使用大的振幅和小的頻率的柏林噪聲函式,同時小的振幅和高的頻率,你可以建立一個平地,另外要建立非常顛簸的平面,應該選擇小的振幅和低的頻率。
在渲染中的應用:
1.在凸凹貼圖它能很好地模擬火焰、雲彩、奇形怪狀的岩石,以及樹木和大理石表面等;
2.做特效地模擬火焰、雲彩等。
比如說立體的柏林噪聲函式
等等內容都是生成我的世界最底層的原理、
64位或者是32位資料溢位也是大概由於bouble函式
引入文章內容
https://zhuanlan.zhihu.com/p/460648846
https://baike.baidu.com/item/%E6%9F%8F%E6%9E%97%E5%99%AA%E5%A3%B0/3366096?fr=aladdin
https://wenku.baidu.com/view/682846054b2fb4daa58da0116c175f0e7cd119c8.html?_wkts_=1679110762667&bdQuery=%E6%9F%8F%E6%9E%97%E5%99%AA%E5%A3%B0%E5%87%BD%E6%95%B0
https://blog.csdn.net/qq_38680728/article/details/122110828
http://www.heathershrewsbury.com/dreu2010/wp-content/uploads/2010/07/AnImageSynthesizer.pdf
https://zhuanlan.zhihu.com/p/228808390
https://dandelioncloud.cn/article/details/1575783317645783042
https://dandelioncloud.cn/article/details/1575743024674336770
https://dandelioncloud.cn/article/details/1575301191817195521
https://space.bilibili.com/247017735?spm_id_from=333.337.search-card.all.click
https://www.bilibili.com/video/BV1gb411r7aE/?spm_id_from=333.788.recommend_more_video.2&;vd_source=d130df1eedc2e3093b7f60c0f41a865a